Sparse Table: A Powerful Data Structure for Efficient Range Queries

• The Sparse Table is a data structure used to efficiently answer range queries on a static array.
• It is used for frequent range queries, such as finding the minimum, maximum, sum, or any other associative operation over a subarray.
• It allows us to perform range queries in O(1) time complexity while having a preprocessing time of O(n log n).
• This makes it an excellent choice for scenarios where the array is static or changes infrequently.

The Sparse Table Basically Stores 2i-th Parent of Nodes

• Let's try to construct a Sparse Table for the following Binary Tree.

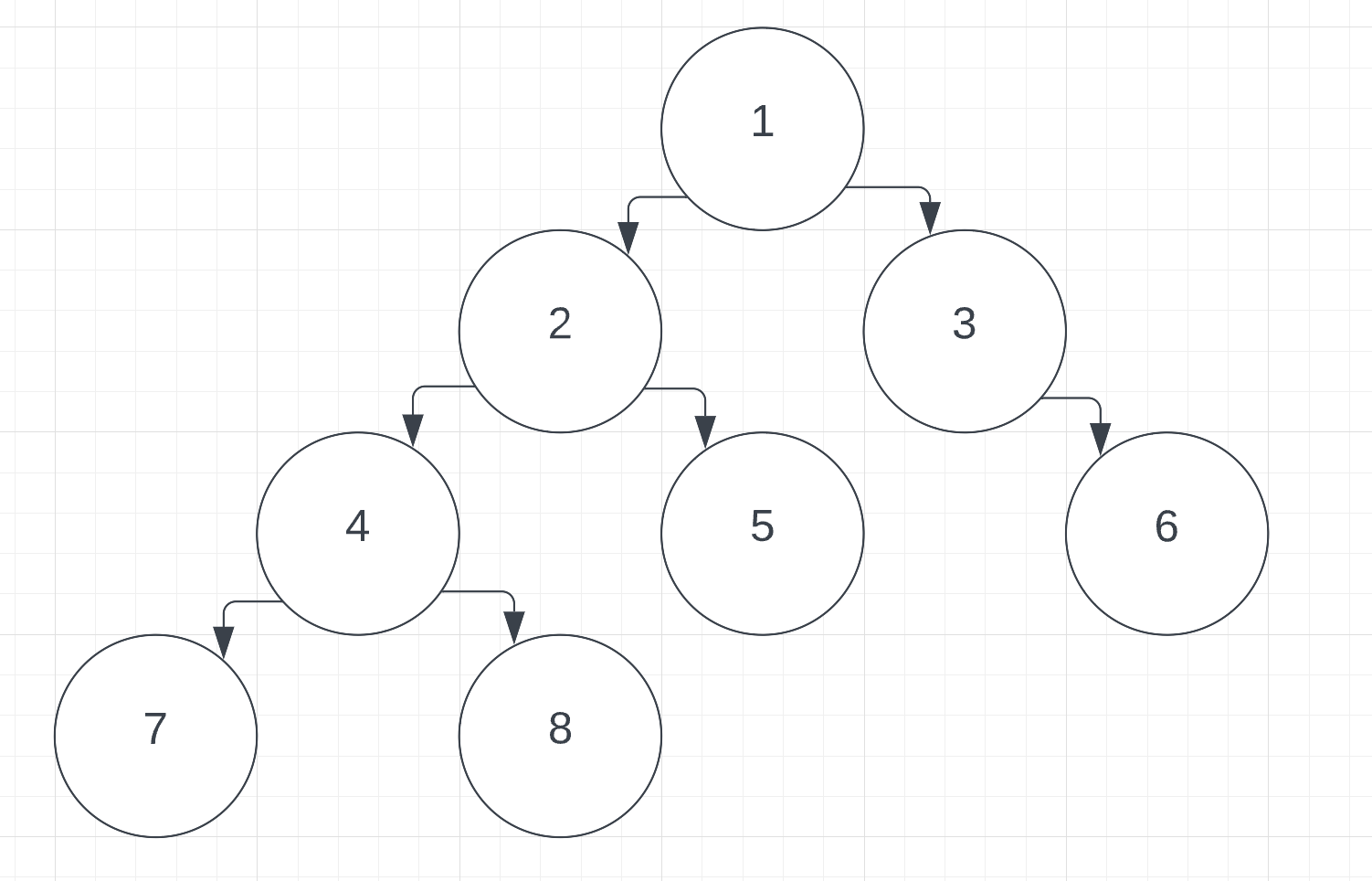
We can see that

• Node 1 is root hence it has no parent. Let default parent be 0.
• Node 2 and 3 have 1st parent as 1 and 2nd parent 0.
• Node 4 and 5 have 1st parent as 2 and 2nd parent as 1 and 4th parent as 0.
• Node 6 1st parent as 3 and 2nd parent as 1 and 4th parent as 0.
• Node 7 and 8 have 1st parent as 4 and 2nd parent as 2 and 4th parent as 0.

Basically we want to look at 2i-th parent of every node and store it in a table.

• Hence the Sparce Table for this Binary Tree will look like :

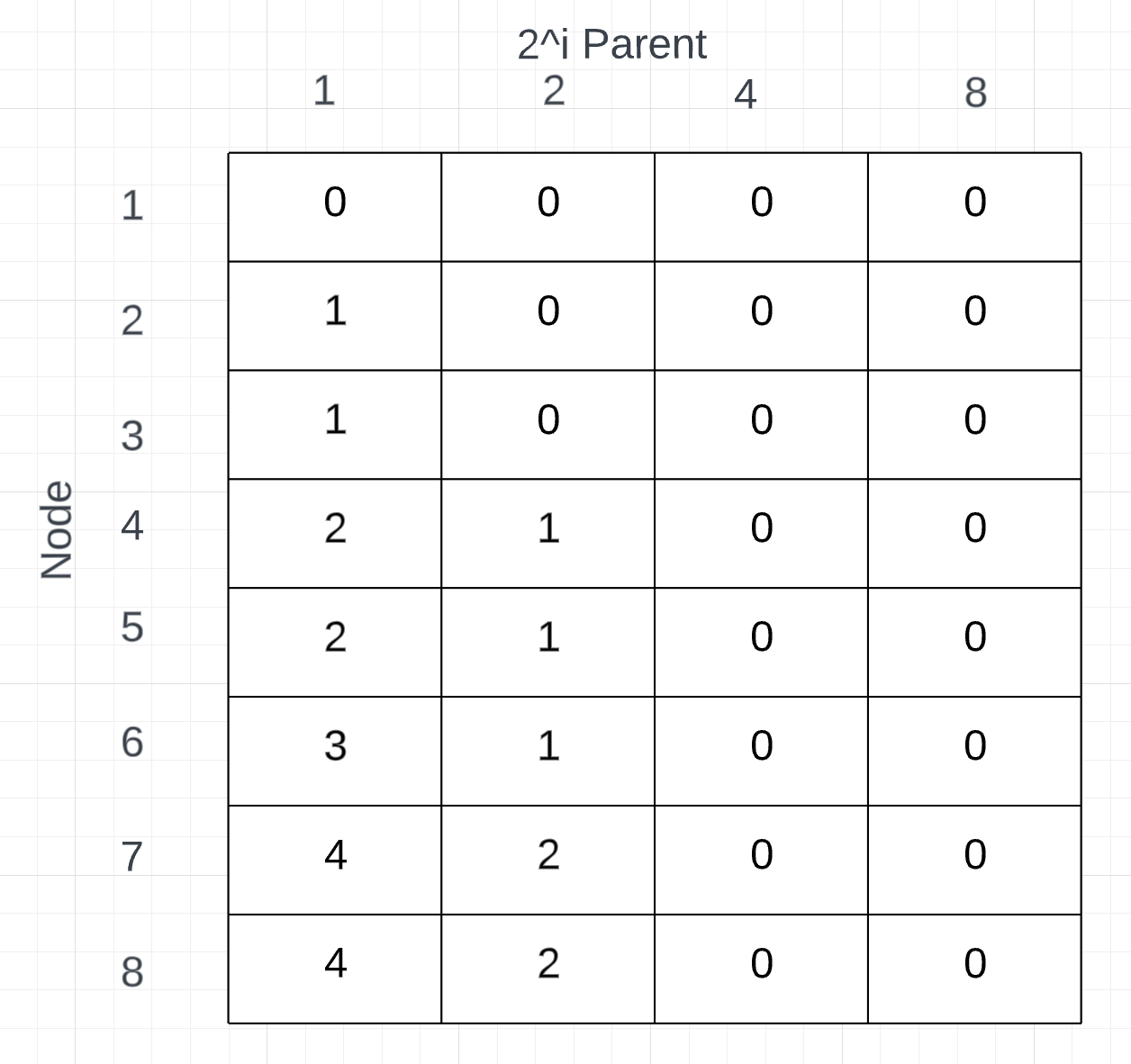
Coding Sparse Table

Python Code :

class Sparse_Table:
    def __init__(self, graph: dict):
        self.M = int(math.log2(len(graph)+3) + 2)
        self.parent = [[0]*self.M for _ in range(len(graph)+3)]
        self.depth = [0]*(len(graph)+3)
        self.dfs(graph)

    def dfs(self, graph: dict):
        def dfs1(curr: int, par: int):
            self.parent[curr][0] = par
            self.depth[curr] = self.depth[par] + 1
            for j in range(1, self.M):
                self.parent[curr][j] = self.parent[self.parent[curr][j-1]][j-1]
            for child in graph[curr]:
                if child != par:
                    dfs1(child, curr)
        dfs1(1, 0)

---

Common Applications of Sparce Table

• Range Minimum/Maximum Query (RMQ): Sparse tables can be used to solve the RMQ problem efficiently. They can answer queries for finding the minimum or maximum value in a given range of an array in O(1) time after O(n log n) preprocessing, where n is the size of the array.

import math

class RMQ:
    def __init__(self, arr):
        self.arr = arr
        self.n = len(arr)
        self.lookup = [[0 for i in range(self.n)] for j in range(self.n)]
        self.buildSparseTable()

    def buildSparseTable(self):
        for i in range(0, self.n):
            self.lookup[i][0] = self.arr[i]
        j = 1
        while (1 << j) <= self.n:
            i = 0
            while (i + (1 << j) - 1) < self.n:
                if self.lookup[i][j - 1] < self.lookup[i + (1 << (j - 1))][j - 1]:
                    self.lookup[i][j] = self.lookup[i][j - 1]
                else:
                    self.lookup[i][j] = self.lookup[i + (1 << (j - 1))][j - 1]
                i += 1
            j += 1

    def query(self, L, R):
        j = int(math.log2(R - L + 1))
        if self.lookup[L][j] <= self.lookup[R - (1 << j) + 1][j]:
            return self.lookup[L][j]
        else:
            return self.lookup[R - (1 << j) + 1][j]

---

• Range Sum Query (RSQ): Sparse tables can also be used to solve the RSQ problem, which involves finding the sum of elements in a given range of an array. They can answer queries for range sums in O(1) time after O(n log n) preprocessing.

• Lowest Common Ancestor (LCA): Sparse tables can be applied to efficiently find the lowest common ancestor of two nodes in a tree. By precomputing information about the tree, sparse tables can answer LCA queries in O(1) time after O(n log n) preprocessing.

class LCA:
    def __init__(self, graph: dict):
        self.table = Sparse_Table(graph)

    # Returns the LCA of Nodes U and V
    def getLCA(self, u: int, v: int):
        if self.table.depth[u] < self.table.depth[v]:
            u, v = v, u
        diff = self.table.depth[u] - self.table.depth[v]
        for i in range(self.table.M-1, -1, -1):
            if (diff >> i) & 1:
                u = self.table.parent[u][i]
        if u == v:
            return u
        for i in range(self.table.M-1, -1, -1):
            if self.table.parent[u][i] != self.table.parent[v][i]:
                u = self.table.parent[u][i]
                v = self.table.parent[v][i]
        return self.table.parent[u][0]

    Returns the Distance between U and V
    def dist(self, u: int, v: int):
        return self.table.depth[u] + self.table.depth[v] - 2*self.table.depth[self.getLCA(u, v)]

---

• Range Mode Query: Sparse tables can be extended to find the mode (most frequent element) in a given range of an array efficiently. By storing additional information during preprocessing, sparse tables can answer mode queries in O(1) time after O(n log n) preprocessing.

• Range GCD/LCM Query: Sparse tables can be used to find the greatest common divisor (GCD) or least common multiple (LCM) of a given range of elements in an array. They can answer GCD/LCM queries in O(1) time after O(n log n) preprocessing.

import math

class Range_GCD_Query:
    def __init__(self, arr):
        self.arr = arr
        self.n = len(arr)
        self.lookup = [[0 for i in range(self.n)] for j in range(self.n)]
        self.buildSparseTable()

    def buildSparseTable(self):
        for i in range(0, self.n):
            self.lookup[i][0] = self.arr[i]
        j = 1
        while (1 << j) <= self.n:
            i = 0
            while (i + (1 << j) - 1) < self.n:
                self.lookup[i][j] = math.gcd(
                    self.lookup[i][j - 1], self.lookup[i + (1 << (j - 1))][j - 1])
                i += 1
            j += 1

    def query(self, L, R):
        j = int(math.log2(R - L + 1))
        return math.gcd(self.lookup[L][j], self.lookup[R - (1 << j) + 1][j])

---

• Range Kth Smallest/Largest Query: Sparse tables can be employed to find the Kth smallest or largest element in a given range of an array. By storing additional information during preprocessing, sparse tables can answer Kth smallest/largest queries in O(1) time after O(n log n) preprocessing.