In this blog, I will be discussing about various Overlapping Interval Problems and how we can solve them.

Interval overlapping problems in competitive programming involve manipulating intervals (ranges) and determining if they overlap with each other. The goal is to design an efficient algorithm to solve these problems.

The general idea to solve interval overlapping problems is to sort the intervals based on their start or end points and then traverse them to identify the overlaps. Here's a step-by-step approach:

Problems Related to Overlapping Intervals :

1. Maximum Number of Overlapping Intervals

Find the maximum number of intervals that overlap with each other.

Example Problems :Given two arrays, $arrival[]$ and $departure[]$, representing the arrival and departure times of trains at a railway station, find the maximum number of platforms required to accommodate all the trains.

Sample Input :

$arrival = [900, 940, 950, 1100, 1500, 1800]$ $departure = [910, 1200, 1120, 1130, 1900, 2000]$

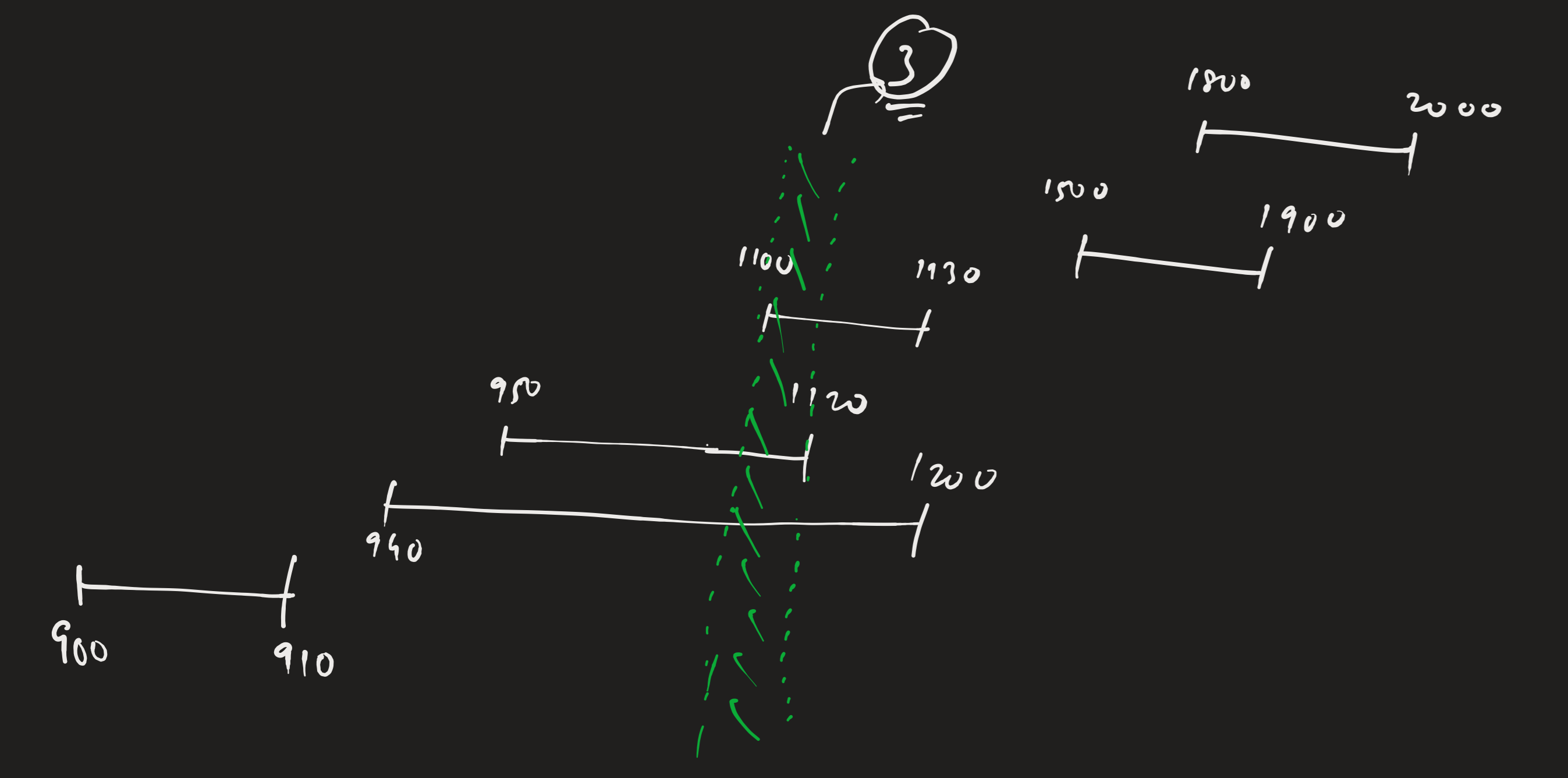
Description of image

From this digram it is clear that we want to find the maximum number of intervals overlapping at a time. That is our answer.

Brute Force Approach:

We can initialize an array $x=[0,0,...]$
For every Interval $(t_1,t_2)$, we will perform $x[t_1] = x[t_1]+1$ and $x[t_1+1] = x[t_1+1]+1$,..$x[t_2] = x[t_2]+1$
After processing all intervals we can find the maximum element in X and that will be our answer.
This will cost $O(Q.N)$ where N is length of X and Q is number of intervals.

There are different ways to solve such problems Optimally. Lets try to understand each one :

Difference Array And Prefix Sums

For each query When we all +1 to the range $[t_1,t_2]$, we waste a lot of time.
We can make use of Difference array and Prefix Sum to Optimize it to $O(N+Q)$.
Let $X = [0,0,...N times]$.
Let a difference array $D$ of $X$ such that $D_i = X_i - X_{i-1}$.
We can see that for every $(t1,t2)$ we can do operation $D[t_1-1]+=1$ and $D[t_2+1]-=1$ in $O(1)$
From this array D, we can obtain X by taking Prefix Sum of D.

Example Code:

def max_platforms(arrival, departure):
    # Create a difference array
    diff = [0] * (max(departure) + 2)

    # Increment arrival time index and decrement departure time index
    for i in range(len(arrival)):
        diff[arrival[i]] += 1
        diff[departure[i] + 1] -= 1

    # Calculate prefix sums
    prefix_sum = [0] * len(diff)
    prefix_sum[0] = diff[0]
    for i in range(1, len(diff)):
        prefix_sum[i] = prefix_sum[i - 1] + diff[i]

    # Return the maximum value in the prefix sums
    return max(prefix_sum)

We can also use Sweep Line Algorithm

Code:

def find_max_platforms(arrival, departure):
    events = []
    for i in range(len(arrival)):
        events.append((arrival[i], 'arr'))
        events.append((departure[i], 'dep'))
    events.sort(key=lambda x: x[0])  # Sort events by time
    max_platforms = 0
    platforms = 0
    for event in events:
        if event[1] == 'arr':
            platforms += 1  # Train arrival
            max_platforms = max(max_platforms, platforms)
        else:
            platforms -= 1  # Train departure
    return max_platforms

2. Maximum Subset of Non-Overlapping Intervals

Find the largest subset of intervals that do not overlap with each other.

Example Problems

Given a set of intervals, you are tasked with finding the largest subset of intervals that do not overlap with each other. In other words, you need to select the maximum number of intervals such that no two intervals in the subset overlap.

Formally, you are given a collection of intervals I = [(a1, b1), (a2, b2), ..., (an, bn)], where each interval is defined by its start and end points. Your goal is to find the largest subset S of intervals from I such that for any two intervals (ai, bi) and (aj, bj) in S, it holds that bi < aj or bj < ai (i.e., the intervals do not overlap).

For example, consider the following set of intervals: I = [(1, 4), (3, 6), (2, 8), (5, 9), (7, 10)]

In this case, the largest subset of non-overlapping intervals is S = [(1, 4), (5, 9), (7, 10)], with a total of 3 intervals.

Your task is to devise an efficient algorithm that solves this problem and returns the size of the largest non-overlapping subset of intervals.

Note: There can be multiple valid solutions with the same maximum size. Your algorithm only needs to return the size of the subset, not the actual intervals themselves.

def maxNonOverlappingSubset(intervals):
    intervals.sort(key=lambda x: x[1]) # Sort by End Time
    count = 0  
    lastEnd = float('-inf') 

    for interval in intervals:
        start, end = interval
        if start > lastEnd:
            count += 1
            lastEnd = end

    return count

3. Minimum Number of Intervals to Remove

Determine the minimum number of intervals that need to be removed to make all intervals non-overlapping.

Example Problem:

Given a set of intervals, find the minimum number of intervals that need to be removed in order to make all intervals non-overlapping.

def eraseOverlapIntervals(intervals):
    if not intervals:
        return 0
    
    intervals.sort(key=lambda x: x[1])  # Sort intervals based on end points in ascending order
    count = 0
    end = intervals[0][1]  # Initialize end point with the first interval
    
    for i in range(1, len(intervals)):
        if intervals[i][0] < end:
            count += 1  # Current interval overlaps with previous interval, increment count
        else:
            end = intervals[i][1]  # Update end point to the current interval's end point
    
    return count

4. Merge Overlapping Intervals

Merge intervals that overlap with each other into a consolidated set of non-overlapping intervals

Example Problem: The popular problem of merging overlapping intervals involves taking a collection of intervals and merging any intervals that overlap with each other. The goal is to produce a consolidated set of non-overlapping intervals.

Sorting Approach

Sort the intervals based on their start times in ascending order.

Initialize an empty result list and add the first interval to it.
Iterate through the remaining intervals, and for each interval:
- If its start time is less than or equal to the end time of the last interval in the result list, merge the intervals by updating the end time of the last interval in the result list if necessary.
- Otherwise, add the interval to the result list.
Return the result list containing the merged intervals.

This approach has a time complexity of $O(n log n)$ due to the sorting step, where n is the number of intervals.

def merge_intervals(intervals):
    # Sort the intervals based on start times
    intervals.sort(key=lambda x: x[0])

    merged = []
    for interval in intervals:
        # If the merged list is empty or the current interval doesn't overlap with the last merged interval
        if not merged or interval[0] > merged[-1][1]:
            merged.append(interval)
        else:
            # Update the end time of the last merged interval if necessary
            merged[-1][1] = max(merged[-1][1], interval[1])
    return merged

Sweepline Approach

Create two arrays: one for storing the start times of intervals and another for storing the end times.
Populate the start and end time arrays with the respective values from the intervals.
Sort both arrays together, maintaining the correspondence between start and end times.
Initialize an empty result list and set two pointers, one for the start array and one for the end array, to 0.
Iterate through the sorted arrays simultaneously, and for each value:
- If it corresponds to a start time, increment a counter.
- If it corresponds to an end time, decrement the counter.
- If the counter becomes zero, it means all intervals in the current range have been accounted for, so create a merged interval from the start time at the beginning of the range and the current end time. Add this merged interval to the result list.
Return the result list containing the merged intervals.

This approach has a time complexity of O(n log n) due to the sorting step, where n is the number of intervals.

def merge_intervals(intervals):
    # Create arrays for start times and end times
    start_times = [interval[0] for interval in intervals]
    end_times = [interval[1] for interval in intervals]
    # Combine and sort the start and end times together
    combined_times = sorted(start_times + end_times)
    merged = []
    counter = 0
    start = None
    for time in combined_times:
        if time in start_times:
            counter += 1
            if counter == 1:
                start = time
        else:
            counter -= 1
            if counter == 0:
                merged.append([start, time])
    return merged

5. Interval Intersection:

Find the intersection (common region) of two or more intervals.

Example Problem: A popular problem involving interval intersection is to find the common region or intersection of two or more intervals. This problem arises in various domains, such as scheduling, time management, and resource allocation. The task is to determine the range of values that are present in all given intervals.

Sweepline Approach

This algorithm involves scanning the intervals from left to right, maintaining a list of active intervals at any given point.

We start by sorting all the interval endpoints.
As we scan the intervals, we add them to the active list when their start point is encountered and remove them when their end point is reached.
At each point, we check if the number of active intervals is greater than or equal to the desired number of intervals (e.g., 2 for finding the intersection of two intervals).
If so, we have an intersection. This algorithm has a time complexity of $O(n log n)$, where n is the total number of interval endpoints.

def interval_intersection(intervals):
    if not intervals:
        return []
    # Sort intervals based on start points
    sorted_intervals = sorted(intervals, key=lambda x: x[0])

    result = []
    curr_start, curr_end = sorted_intervals[0]

    for interval in sorted_intervals[1:]:
        if interval[0] <= curr_end:
            # Overlapping interval
            curr_start = max(curr_start, interval[0])
            curr_end = min(curr_end, interval[1])
        else:
            # Non-overlapping interval, add intersection if any
            if curr_start <= curr_end:
                result.append([curr_start, curr_end])
            curr_start, curr_end = interval

    # Add the last intersection if any
    if curr_start <= curr_end:
        result.append([curr_start, curr_end])

    return result

Interval Trees

If we wish to find the intervals that intersect with a particular interval, we can use interval trees.

class IntervalTreeNode:
    def __init__(self, interval):
        self.interval = interval
        self.max_end = interval[1]
        self.left = None
        self.right = None


class IntervalTree:
    def __init__(self):
        self.root = None

    def insert(self, interval):
        if not self.root:
            self.root = IntervalTreeNode(interval)
        else:
            self._insert_helper(self.root, interval)

    def _insert_helper(self, node, interval):
        node.max_end = max(node.max_end, interval[1])

        if interval[0] < node.interval[0]:
            if node.left:
                self._insert_helper(node.left, interval)
            else:
                node.left = IntervalTreeNode(interval)
        else:
            if node.right:
                self._insert_helper(node.right, interval)
            else:
                node.right = IntervalTreeNode(interval)

    def interval_intersection(self, interval):
        result = []
        self._interval_intersection_helper(self.root, interval, result)
        return result

    def _interval_intersection_helper(self, node, interval, result):
        if not node:
            return

        if interval[0] <= node.interval[1] and interval[1] >= node.interval[0]:
            result.append(node.interval)

        if node.left and node.left.max_end >= interval[0]:
            self._interval_intersection_helper(node.left, interval, result)

        if node.right and node.right.interval[0] <= interval[1]:
            self._interval_intersection_helper(node.right, interval, result)

Example Usage:

intervals = [[1, 4], [3, 6], [8, 10], [9, 12]]

search_interval = [2, 7]

tree = IntervalTree()

for interval in intervals:
    tree.insert(interval)

result = tree.interval_intersection(search_interval)

print("Intervals Intersecting with", search_interval, "are", result)
# Intervals Intersecting with [2, 7] are [[1, 4], [3, 6]]

6. Interval Partitioning / Activity Selection Problems :

Divide a set of intervals into a minimum number of disjoint subsets, where no intervals in the same subset overlap.

Example Problem: The problem of interval partitioning, also known as the activity selection problem, involves dividing a set of intervals into a minimum number of disjoint subsets, where no intervals in the same subset overlap. This problem has various applications, such as scheduling tasks, allocating resources, and organizing events. The goal is to find an efficient solution that minimizes the number of subsets required.

Greedy Approach

def interval_partitioning(intervals):
    # Sort intervals based on their end times
    sorted_intervals = sorted(intervals, key=lambda x: x[1])

    # Initialize the first subset with the earliest interval
    subsets = [[sorted_intervals[0]]]

    # Iterate through the remaining intervals
    for interval in sorted_intervals[1:]:
        # Check if the interval overlaps with any intervals in the existing subsets
        for subset in subsets:
            if interval[0] >= subset[-1][1]:
                # Add the interval to the subset if it doesn't overlap
                subset.append(interval)
                break
        else:
            # If the interval overlaps with all existing subsets, create a new subset
            subsets.append([interval])

    return subsets

7. Interval Coloring:

Assign colors to a set of intervals such that no two overlapping intervals have the same color.

Greedy Approach

def interval_coloring(intervals):
    intervals.sort(key=lambda x: x[0])  # Sort intervals based on start times
    colors = []  # List to store the assigned colors

    for interval in intervals:
        # Check for available colors that don't conflict with overlapping intervals
        available_colors = set(range(1, len(colors) + 2))

        for i in range(len(colors)):
            if intervals[i][1] >= interval[0]:  # If intervals overlap
                available_colors.discard(colors[i])

        if not available_colors:
            # If no available colors, create a new color and assign it
            colors.append(len(colors) + 1)
        else:
            # Assign the minimum available color to the interval
            colors.append(min(available_colors))

    return colors