Computing the Sum of Euler's Totient Function Efficiently
Written on November 26, 2024
Views : Loading...
Introduction
Euler's Totient Function, denoted as $\varphi(n)$, is a fundamental concept in number theory. It counts the positive integers up to a given integer $n$ that are relatively prime to $n$. The function has significant applications in cryptography, particularly in RSA encryption, and in solving problems related to primitive roots and modular arithmetic.
Computing the sum of Euler's Totient Function up to a large number $N$, represented as $\Phi(N) = \sum_{i=1}^{N} \varphi(i)$, is a common problem in computational number theory. Naively computing this sum is inefficient for large $N$ due to the computational complexity of calculating $\varphi(n)$ for each $n$. In this blog post, we will delve into an efficient algorithm that computes $\Phi(N)$ in $O\left(N^{2/3} (\log\log{N})^{1/3}\right)$ time, making it practical for large-scale computations.
Understanding Euler's Totient Function
Definition
For a positive integer $n$, Euler's Totient Function $\varphi(n)$ is defined as the number of integers $k$ in the range $1 \leq k \leq n$ such that $\gcd(n, k) = 1$. In other words, it counts the numbers less than or equal to $n$ that are coprime to $n$.
Example:
- For $n = 9$, the numbers less than or equal to $9$ that are coprime to $9$ are $1, 2, 4, 5, 7, 8$.
- Therefore, $\varphi(9) = 6$.
Properties
-
Multiplicative Property:
If $m$ and $n$ are coprime, then: $$ \varphi(mn) = \varphi(m) \cdot \varphi(n). $$
-
Formula for Prime Powers:
If $p$ is a prime number and $k \geq 1$, then: $$ \varphi(p^k) = p^k - p^{k-1} = p^{k-1}(p - 1). $$
-
General Formula:
For any positive integer $n$ with prime factorization $n = p_1^{e_1} p_2^{e_2} \cdots p_r^{e_r}$, $$ \varphi(n) = n \prod_{i=1}^r \left(1 - \frac{1}{p_i}\right). $$
The Challenge of Summing $\varphi(n)$
Computing the sum $\Phi(N) = \sum_{i=1}^{N} \varphi(i)$ directly involves calculating $\varphi(n)$ for each $n$ up to $N$. Using the naive approach, this requires $O(N \log \log N)$ time, as calculating each $\varphi(n)$ takes $O(\log \log n)$ time using a modified sieve. For large $N$, this becomes computationally expensive.
Our goal is to find an algorithm that reduces the time complexity to $O\left(N^{2/3} (\log\log{N})^{1/3}\right)$.
Deriving the Efficient Algorithm
To compute $\Phi(N)$ efficiently, we will leverage Dirichlet Convolution and Möbius Inversion, fundamental tools in number theory that allow us to relate multiplicative functions and invert summatory relations. This approach will lead us to a recursive formula that expresses $\Phi(N)$ in terms of smaller values of $\Phi(n)$. We will detail each mathematical step thoroughly.
Step 1: Establishing a Key Identity
We start by recalling a fundamental identity involving Euler's Totient Function:
$$ \varphi(n) = \sum_{d \mid n} \mu(d) \cdot \frac{n}{d}, $$
where $\mu(d)$ is the Möbius function, and the sum is over all positive divisors $d$ of $n$.
Dirichlet Convolution Context:
In the language of Dirichlet convolution, this identity can be written as:
$$ \varphi = \mu * \text{id}, $$
where $\text{id}(n) = n$ is the identity function, and $*$ denotes Dirichlet convolution.
Step 2: Summing the Identity Over All Integers Up to $N$
Our goal is to compute:
$$ \Phi(N) = \sum_{n=1}^{N} \varphi(n). $$
Substituting the key identity into this sum:
$$ \Phi(N) = \sum_{n=1}^{N} \sum_{d \mid n} \mu(d) \cdot \frac{n}{d}. $$
Step 3: Interchanging the Order of Summation
To simplify the double sum, we interchange the order of summation:
$$ \Phi(N) = \sum_{d=1}^{N} \mu(d) \cdot \sum_{\substack{n=1 \ d \mid n}}^{N} \frac{n}{d}. $$
Explanation:
- For each divisor $d$, we sum over all multiples of $d$ up to $N$.
- Let $k = \frac{n}{d}$, where $k$ runs from $1$ to $\left\lfloor \frac{N}{d} \right\rfloor$.
Thus, the inner sum becomes:
$$ \sum_{\substack{n=1 \ d \mid n}}^{N} \frac{n}{d} = \sum_{k=1}^{\left\lfloor \frac{N}{d} \right\rfloor} k = \frac{\left\lfloor \frac{N}{d} \right\rfloor \cdot \left(\left\lfloor \frac{N}{d} \right\rfloor + 1\right)}{2}. $$
Therefore,
$$ \Phi(N) = \sum_{d=1}^{N} \mu(d) \cdot \frac{\left\lfloor \frac{N}{d} \right\rfloor \cdot \left(\left\lfloor \frac{N}{d} \right\rfloor + 1\right)}{2}. $$
Step 4: Simplifying the Summation
We can factor out constants and rewrite the summation:
$$ \Phi(N) = \frac{1}{2} \sum_{d=1}^{N} \mu(d) \cdot \left\lfloor \frac{N}{d} \right\rfloor \cdot \left(\left\lfloor \frac{N}{d} \right\rfloor + 1\right). $$
This formula allows us to compute $\Phi(N)$ directly. However, computing this sum naively would still require $O(N)$ operations, which is not efficient enough for large $N$. To optimize, we need to find a recursive relation that reduces the number of computations.
Step 5: Establishing a Recursive Formula Using Möbius Inversion
To derive a recursive formula for $\Phi(N)$, we start by considering the sum of Euler's Totient Function over its divisors.
Fundamental Identity:
$$ \sum_{d \mid n} \varphi(d) = n. $$
Summing Over All $n$ Up to $N$:
$$ \sum_{n=1}^{N} \sum_{d \mid n} \varphi(d) = \sum_{n=1}^{N} n = \frac{N(N + 1)}{2}. $$
Interchanging the Order of Summation:
$$ \sum_{d=1}^{N} \varphi(d) \cdot \left\lfloor \frac{N}{d} \right\rfloor = \frac{N(N + 1)}{2}. $$
Expressing $\Phi(N)$:
Recall that:
$$ \Phi(N) = \sum_{d=1}^{N} \varphi(d). $$
Our goal is to express $\Phi(N)$ in terms of $\Phi\left(\left\lfloor \frac{N}{d} \right\rfloor\right)$ for smaller values of $N$.
Rearranging the Summation:
We can write:
$$ \sum_{d=1}^{N} \varphi(d) \cdot \left\lfloor \frac{N}{d} \right\rfloor = \sum_{d=1}^{N} \varphi(d) \cdot \left( \frac{N}{d} - \lbrace \frac{N}{d} \rbrace \right) = N \sum_{d=1}^{N} \frac{\varphi(d)}{d} - \sum_{d=1}^{N} \varphi(d) \lbrace \frac{N}{d} \rbrace, $$
where $\lbrace x \rbrace$ denotes the fractional part of $x$.
However, dealing with the fractional parts complicates the expression. Instead, we can approach the problem by recognizing that many terms $\left\lfloor \frac{N}{d} \right\rfloor$ repeat for different values of $d$. This observation allows us to group terms and reduce computational complexity.
Key Insight:
For a given integer $k$, the number of times $\left\lfloor \frac{N}{d} \right\rfloor = k$ occurs corresponds to the number of divisors $d$ such that $k = \left\lfloor \frac{N}{d} \right\rfloor$. This grouping significantly reduces the number of unique terms in the summation.
Step 6: Applying Dirichlet Convolution and Möbius Inversion
To derive a recursive relation, we leverage the properties of Dirichlet convolution and Möbius inversion.
Recall the Fundamental Identity:
$$ \sum_{d \mid n} \varphi(d) = n. $$
In Dirichlet convolution terms, this is:
$$ \varphi * 1 = \text{id}, $$
where $\text{id}(n) = n$.
Applying Möbius Inversion:
Möbius inversion allows us to invert such convolution relations. Specifically, if:
$$ f * g = h, $$
then:
$$ f = h * \mu, $$
provided that $g * \mu = \epsilon$, where $\epsilon(n)$ is the identity element for Dirichlet convolution ($\epsilon(1) = 1$, and $\epsilon(n) = 0$ for $n > 1$).
Applying Möbius inversion to our identity:
$$ \varphi = \text{id} * \mu. $$
Summing Both Sides:
Summing $\varphi(n)$ up to $N$ gives:
$$ \Phi(N) = \sum_{n=1}^{N} \varphi(n) = \sum_{n=1}^{N} \sum_{d \mid n} \mu(d) \cdot \frac{n}{d}. $$
Interchanging the order of summation:
$$ \Phi(N) = \sum_{d=1}^{N} \mu(d) \cdot \sum_{k=1}^{\left\lfloor \frac{N}{d} \right\rfloor} k = \sum_{d=1}^{N} \mu(d) \cdot \frac{\left\lfloor \frac{N}{d} \right\rfloor \cdot \left(\left\lfloor \frac{N}{d} \right\rfloor + 1\right)}{2}. $$
Step 7: Establishing the Recursive Relation
While the above formula provides a direct computation of $\Phi(N)$, it involves $O(N)$ operations. To achieve our target time complexity of $O\left(N^{2/3} (\log\log{N})^{1/3}\right)$, we need a more efficient approach.
Recursive Formula:
We can derive a recursive relation for $\Phi(N)$ based on the following identity:
$$ \sum_{d=1}^{N} \varphi(d) \cdot \left\lfloor \frac{N}{d} \right\rfloor = \frac{N(N + 1)}{2}. $$
Rearranging the terms:
$$ \Phi(N) = \frac{N(N + 1)}{2} - \sum_{d=2}^{N} \varphi(d) \cdot \left\lfloor \frac{N}{d} \right\rfloor. $$
However, directly computing this sum is inefficient. Instead, we observe that the values $\left\lfloor \frac{N}{d} \right\rfloor$ repeat for consecutive ranges of $d$. This allows us to group the summation terms based on the unique values of $\left\lfloor \frac{N}{d} \right\rfloor$.
Grouping Terms:
Let $k = \left\lfloor \frac{N}{d} \right\rfloor$. For each unique $k$, determine the range of $d$ values that produce the same $k$. Specifically:
$$ d \in \left( \frac{N}{k + 1}, \frac{N}{k} \right]. $$
The number of unique $k$ values is $O(N^{1/2})$, as for larger $k$, the intervals become narrower.
Final Recursive Formula:
By leveraging the above grouping, we arrive at the recursive formula:
$$ \Phi(N) = \frac{N(N + 1)}{2} - \sum_{k=2}^{\left\lfloor \frac{N}{2} \right\rfloor} \Phi\left( \left\lfloor \frac{N}{k} \right\rfloor \right). $$
Explanation:
- The term $\frac{N(N + 1)}{2}$ represents the sum of the first $N$ natural numbers.
- The summation $\sum_{k=2}^{\left\lfloor \frac{N}{2} \right\rfloor} \Phi\left( \left\lfloor \frac{N}{k} \right\rfloor \right)$ accounts for the overcounting in the initial summation by recursively subtracting contributions from smaller intervals.
This recursive relation significantly reduces the number of computations by reusing previously computed values of $\Phi(n)$ for smaller $n$.
Step 8: Implementing the Algorithm
With the recursive formula established, we can now outline the steps to implement the algorithm efficiently.
Precomputing Small Values
- Choose a threshold $k$, typically set as $k = \left( \frac{N}{\log\log N} \right)^{2/3}$.
- Compute $\Phi(n)$ for all $n \leq k$ using a modified sieve algorithm.
Sieve Algorithm for $\varphi(n)$:
- Initialize an array
phi[1..k]withphi[i] = ifor all $i$. - For each prime $p \leq k$:
- For multiples of $p$, set: $$ \phi[j] = \phi[j] - \frac{\phi[j]}{p}. $$
- Accumulate the values to compute $\Phi(n)$:
- For $n$ from $1$ to $k$: $$ \Phi(n) = \Phi(n - 1) + \varphi(n). $$
This precomputes $\Phi(n)$ for $n \leq k$ in $O(k \log\log k)$ time.
Recursive Computation for Larger Values
For $n > k$, compute $\Phi(n)$ using the recursive formula:
$$ \Phi(n) = \frac{n(n + 1)}{2} - \sum_{k=2}^{\left\lfloor \frac{n}{2} \right\rfloor} \Phi\left( \left\lfloor \frac{n}{k} \right\rfloor \right). $$
Memoization and Grouping:
To optimize the recursive calls:
- Memoization: Store computed values of $\Phi(n)$ to avoid redundant calculations.
- Grouping: Recognize that many $\left\lfloor \frac{n}{k} \right\rfloor$ values repeat. Group these terms to reduce the number of unique recursive calls.
Algorithm Steps:
- Initialize:
- Precompute $\Phi(n)$ for $n \leq k$ using the sieve.
- Recursion:
- For each $n > k$, compute $\Phi(n)$ using the recursive formula.
- Utilize memoization to store and retrieve previously computed $\Phi(n)$ values.
- Optimization:
- Group similar terms based on unique $\left\lfloor \frac{n}{k} \right\rfloor$ values.
- This reduces the number of recursive computations from $O(n)$ to $O(n^{1/2})$.
Step 9: Time Complexity Analysis
The total time complexity is determined by:
-
Precomputing $\Phi(n)$ for $n \leq k$:
- Time: $O(k \log\log k)$.
-
Computing $\Phi(n)$ for $n > k$:
- Due to grouping and memoization, the number of unique terms is reduced to $O(N^{1/2})$.
- Each computation involves constant-time operations thanks to memoization.
Choosing $k = \left( \frac{N}{\log\log N} \right)^{2/3}$ balances the precomputation and recursive steps, resulting in an overall time complexity of:
$$ O\left( N^{2/3} (\log\log N)^{1/3} \right). $$
This efficient time complexity makes the algorithm practical for large-scale computations of $\Phi(N)$.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
#define int long long int
#define double long double
#define endl '\n'
const int MOD = 998244353;
const int INV2 = 499122177; // Modular inverse of 2 modulo 998244353
const int K = 1000000; // Threshold for precomputation
vector<int> Phi_precomputed(K + 1, 0);
void sieve_phi(vector<int> &phi) {
for(int i = 0; i <= K; ++i){
phi[i] = i;
}
for(int p = 2; p <= K; ++p){
if(phi[p] == p){ // p is prime
for(int multiple = p; multiple <= K; multiple += p){
phi[multiple] -= phi[multiple] / p;
}
}
}
}
unordered_map<int, int> cache;
int compute_Phi(int n, const vector<int> &Phi_precomputed, unordered_map<int, int> &cache){
if(n <= K){
return Phi_precomputed[n];
}
if(cache.find(n) != cache.end()){
return cache[n];
}
int res = ((n % MOD) * ((n + 1) % MOD)) % MOD;
res = (res * INV2) % MOD;
int m = 2;
while(m <= n){
int m_val = n / m;
int upper = n / m_val;
int count = upper - m + 1;
int phi_m = compute_Phi(m_val, Phi_precomputed, cache);
res = (res - ((count % MOD) * phi_m % MOD) + MOD) % MOD;
m = upper + 1;
}
cache[n] = res;
return res;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
vector<int> phi(K + 1, 0);
sieve_phi(phi);
Phi_precomputed[0] = 0;
for(int i = 1; i <= K; ++i){
Phi_precomputed[i] = (Phi_precomputed[i - 1] + phi[i]) % MOD;
}
int result = compute_Phi(n, Phi_precomputed, cache);
cout << result;
return 0;
}
Conclusion
By leveraging Dirichlet Convolution and Möbius Inversion, along with strategic grouping and memoization, we have developed an efficient algorithm to compute the sum of Euler's Totient Function up to a large number $N$. This approach transforms the problem into a recursive relation that significantly reduces computational overhead, achieving a time complexity of $O\left( N^{2/3} (\log\log{N})^{1/3} \right)$. Such optimizations are invaluable in fields like cryptography and computational number theory, where handling large values of $N$ is commonplace.
Further Reading
- Euler's Totient Function: Wikipedia Article
- Number Theory Textbooks:
- An Introduction to the Theory of Numbers by G.H. Hardy and E.M. Wright
- Elementary Number Theory by David M. Burton
- Algorithm Optimization Techniques:
- Introduction to Algorithms by Cormen, Leiserson, Rivest, and Stein
- Project Euler Problems: Project Euler
Share this blog
Related Posts

21-11-2024
A comprehensive guide to understanding derangements using the inclusion and exclusion principle.

20-11-2024
Dive into the fascinating world of combinatorics as we explore the number of ways to tile a $3 \time...

18-11-2024
An in-depth exploration of perfect covers of chessboards using dominoes, including combinatorial rea...
18-05-2025
Learn how to build a robust, serverless application on AWS to perform calculations like $f(x) = x^2 ...
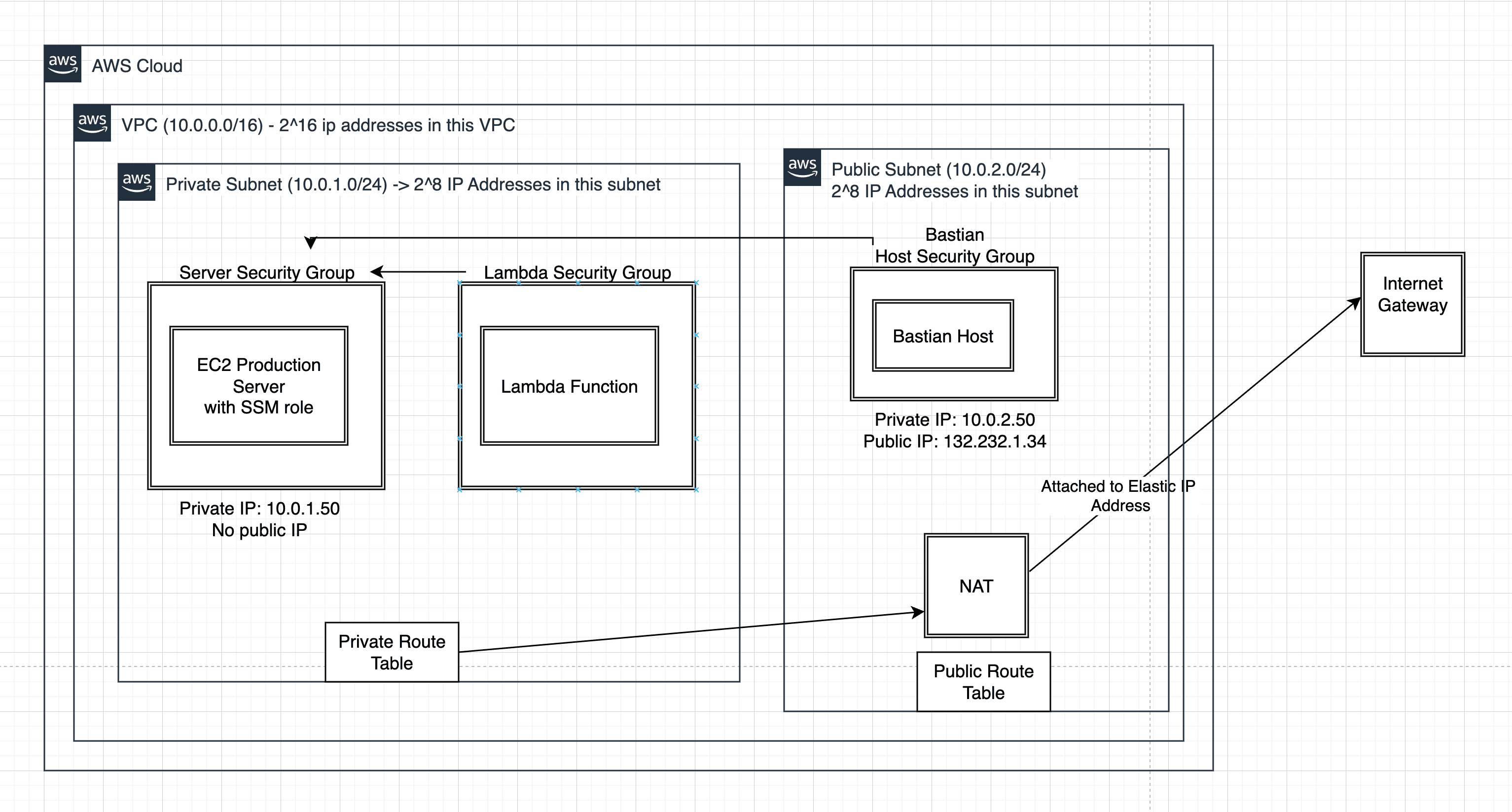
09-02-2025
In this comprehensive blog, discover how to build a production-like AWS environment with a private E...
09-12-2024
This blog is dedicated to simplifying complex mathematical and computational concepts into understan...
01-12-2024
Static Range Sum queries using various Algorithms
30-11-2024
An in-depth exploration of JavaScript iteration methods and best practices in asynchronous programmi...
25-11-2024
In the realm of graph theory, understanding the connectivity of a network is crucial for numerous ap...