Counting Ways to Cover a $3 \times N$ Rectangle with $2 \times 1$ Tiles
Written on November 20, 2024
Views : Loading...

In this blog, we will derive the recurrence relation for the number of ways to tile a $3 \times N$ rectangle with $2 \times 1$ tiles. We’ll break down each step thoroughly to ensure that even someone new to the topic can follow along easily. Let’s dive in!
Understanding the Problem
Imagine you have a rectangle that is 3 units tall and $N$ units wide. Your goal is to cover this entire rectangle using tiles that are $2 \times 1$ blocks. These tiles can be placed either vertically or horizontally.
Our mission is to figure out how many different ways you can arrange these tiles to completely cover the $3 \times N$ rectangle without any overlaps or gaps.
Starting with Simple Cases
Before diving into the general case, let's look at some small values of $N$ to build our understanding.
Case 1: $3 \times 1$ Rectangle
Consider a rectangle that is 3 units tall and 1 unit wide:
| |
| |
| |
- Number of Tiles Needed: To cover a $3 \times 1$ rectangle with $2 \times 1$ tiles, you would need $1.5$ tiles (since $3 \times 1 = 3$ and each tile covers 2 units). But you can't have half a tile!
- Conclusion: 0 ways to tile a $3 \times 1$ rectangle because the number of tiles required is not an integer.
Note: For any odd value of $n$, the number of tiles needed would be a non-integer. Since we can’t have half tiles, there are 0 ways to tile a $3 \times n$ rectangle when $n$ is odd.
Case 2: $3 \times 2$ Rectangle
Now, let’s look at a rectangle that is 3 units tall and 2 units wide:
| | |
| | |
| | |
- Number of Tiles Needed: To cover a $3 \times 2$ rectangle, you need $3$ tiles (since $3 \times 2 = 6$ and each tile covers 2 units).
- Manual Counting: By trying different arrangements, we find that there are 3 distinct ways to tile this rectangle.
Defining Our Function
Let’s define a function to represent the number of ways to tile the rectangle:
- Let $f(n)$ be the number of ways to tile a $3 \times N$ rectangle using $2 \times 1$ tiles.

Visualizing the Tiling Process
To understand how to build up the number of tiling ways for larger $N$, let’s start tiling from the right side of the rectangle and see how different tiling choices affect the remaining space.
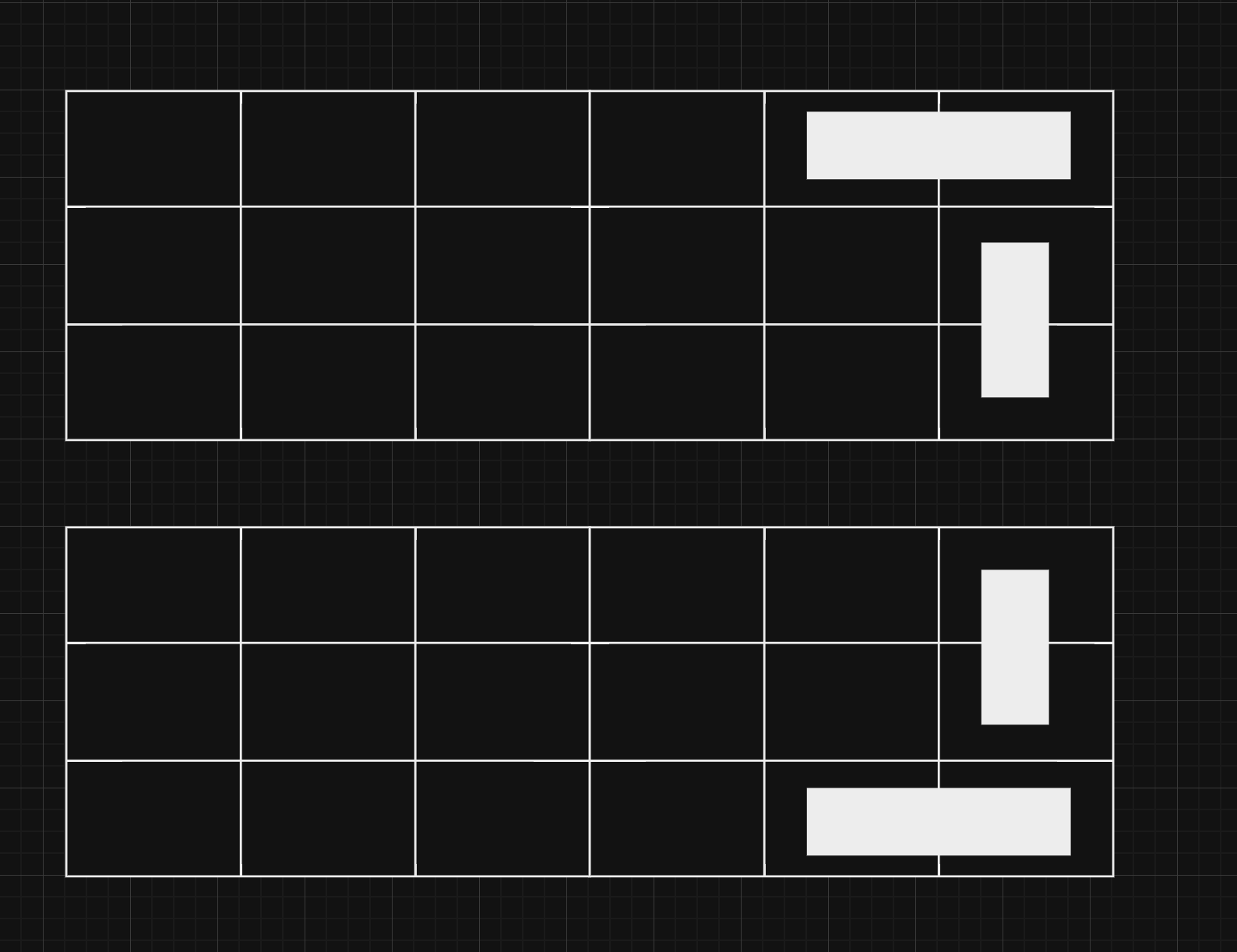
Option 1: All Tiles in the Last Two Columns Are Horizontal
-
Arrangement: Place three horizontal tiles covering the last two columns.
-
Remaining Space: After placing these tiles, we are left with a $3 \times (N-2)$ rectangle.
-
Number of Ways: The number of ways to tile the remaining $3 \times (N-2)$ rectangle is $f(n-2)$.
Figure: Filling the last two columns with horizontal tiles.
Option 2: Other Configurations with Missing Blocks
Sometimes, tiles are placed in such a way that they partially cover the last two columns, leaving one block missing in different positions. These configurations are more complex and require additional considerations.
-
Symmetry Consideration: Due to symmetry, the number of ways to tile these partially covered configurations is the same.
For example, if one tile is placed vertically in one column, it affects the tiling options of adjacent columns.
Figure: Another tiling configuration with partially covered blocks.
-
Introducing $g(n)$: Let’s define another function to represent the number of ways to tile these partially covered configurations.
- Let $g(n)$ be the number of ways to tile a $3 \times N$ rectangle where the last two columns are not fully covered, leaving one block missing.
Establishing the Recurrence Relations
With the above configurations in mind, we can now establish equations that relate $f(n)$ and $g(n)$.
-
For $f(n)$:
- Horizontal Tiles Option: As discussed, placing three horizontal tiles in the last two columns leaves a $3 \times (N-2)$ rectangle, contributing $f(n-2)$ ways.
- Other Configurations: There are two ways to arrange tiles that leave one block missing in different positions, each contributing $g(n-1)$ ways.
Therefore: $$ f(n) = f(n-2) + 2 \times g(n-1) $$
-
For $g(n)$:
- Vertical Tiles Option: Placing a vertical tile affects the next column, leading to $f(n-1)$ ways.
- Other Configurations: Another way to arrange the tiles leads to $g(n-2)$ ways.
Therefore: $$ g(n) = f(n-1) + g(n-2) $$
Figure: Another tiling configuration leading to the relation between $f(n)$ and $g(n)$.
Putting It All Together
Now, we have two equations that relate $f(n)$ and $g(n)$:
-
Main Recurrence for $f(n)$: $$ f(n) = f(n-2) + 2 \times g(n-1) $$
-
Recurrence for $g(n)$: $$ g(n) = f(n-1) + g(n-2) $$
These equations allow us to compute $f(n)$ recursively using previously computed values of $f$ and $g$. This is powerful because it means we can build up the number of tiling ways for larger $N$ step by step, using the solutions to smaller problems.
Solving the Recurrence Relations
To fully solve for $f(n)$, we can use these recurrence relations along with our initial conditions:
- Initial Conditions:
- $f(1) = 0$ (as there are no ways to tile a $3 \times 1$ rectangle)
- $f(2) = 3$ (as there are three ways to tile a $3 \times 2$ rectangle)
- $g(0) = 0$ (no space to tile)
- $g(1) = 1$ (one way to tile a partially covered $3 \times 1$ rectangle)
Using these, we can compute $f(n)$ for any desired $N$.
Example Calculations
Let’s compute $f(4)$ as an example.
-
Using the Recurrence for $f(n)$: $$ f(4) = f(2) + 2 \times g(3) $$
-
Compute $g(3)$ Using Its Recurrence: $$ g(3) = f(2) + g(1) = 3 + 1 = 4 $$
-
Substitute Back to Find $f(4)$: $$ f(4) = 3 + 2 \times 4 = 3 + 8 = 11 $$
So, there are 11 ways to tile a $3 \times 4$ rectangle with $2 \times 1$ tiles.
Lets try eliminating $ g(n) $
Step 1: Express $g(n-1)$ Using the Second Equation
First, let's shift the index in the second equation to express $g(n-1)$ in terms of $f$ and $g$.
Replace $n$ with $(n-1)$ in the second equation: $$ g(n-1) = f(n-2) + g(n-3) $$
Step 2: Substitute $g(n-1)$ Back into the First Equation
Now, substitute this expression for $g(n-1)$ into the first equation: $$ f(n) = f(n-2) + 2 \times g(n-1) $$ $$ f(n) = f(n-2) + 2 \times (f(n-2) + g(n-3)) $$
Step 3: Simplify the Equation
Let's distribute the 2: $$ f(n) = f(n-2) + 2f(n-2) + 2g(n-3) $$ $$ f(n) = 3f(n-2) + 2g(n-3) $$
Step 4: Iteratively Substitute to Eliminate $g(n-3)$
We still have a $g$ term ($g(n-3)$) that we need to eliminate. We'll use the second equation again to express $g(n-3)$ in terms of $f$ and another $g$.
Replace $n$ with $(n-3)$ in the second equation: $$ g(n-3) = f(n-4) + g(n-5) $$
Substitute this back into our equation for $f(n)$: $$ f(n) = 3f(n-2) + 2 \times (f(n-4) + g(n-5)) $$ $$ f(n) = 3f(n-2) + 2f(n-4) + 2g(n-5) $$
Step 5: Continue the Substitution Process
We still have a $g$ term ($g(n-5)$) to eliminate. We'll repeat the substitution process.
Replace $n$ with $(n-5)$ in the second equation: $$ g(n-5) = f(n-6) + g(n-7) $$
Substitute this back into our equation for $f(n)$: $$ f(n) = 3f(n-2) + 2f(n-4) + 2 \times (f(n-6) + g(n-7)) $$ $$ f(n) = 3f(n-2) + 2f(n-4) + 2f(n-6) + 2g(n-7) $$
Step 6: Observing the Pattern
Continuing this process, we notice a pattern forming. Each time we substitute, we introduce a new term $2f(n-2k)$ and a new $g$ term with an increasingly negative index.
After multiple substitutions, the general form becomes: $$ f(n) = 3f(n-2) + 2f(n-4) + 2f(n-6) + \dots + 2f(0) $$
This pattern continues until the $g$ terms are completely eliminated (i.e., when their indices become negative or reach zero).
Step 7: Focusing on Even Values of $n$
Since $f(n) = 0$ for odd $n$, we only need to consider even values of $n$. Let's redefine our function for even indices.
Let $n = 2m$, where $m$ is a non-negative integer. Then, we can denote $f(2m) = f_m$.
Now, our equation becomes: $$ f(2m) = 3f(2m-2) + 2f(2m-4) + 2f(2m-6) + \dots + 2f(0) $$
Step 8: Generalizing the Pattern
Notice that each term after the first one is multiplied by 2. We can express the sum of these terms using sigma (Σ) notation.
The equation can be rewritten as: $$ f(2m) = 3f(2m-2) + 2 \times \left( f(2m-4) + f(2m-6) + \dots + f(0) \right) $$ $$ f(2m) = 3f(2m-2) + 2 \times \sum_{k=0}^{m-2} f(2k) $$
However, to align with the desired form, we'll adjust the indexing.
Step 9: Adjusting the Indexing
Let's shift the index in the summation to include all terms up to $f(2m)$.
Consider $f(2m+2)$: $$ f(2m+2) = 3f(2m) + 2 \times \left( f(2m-2) + f(2m-4) + \dots + f(0) \right) $$ $$ f(2m+2) = 3f(2m) + 2 \times \sum_{k=0}^{m} f(2k) $$
Here, the summation $\sum_{k=0}^{m} f(2k)$ represents the sum of all $f$ terms from $f(0)$ up to $f(2m)$ in increments of 2.
Step 10: Final Recurrence Relation
Replacing $m$ with $n$ for simplicity, we obtain the final recurrence relation: $$ f(2n + 2) = 3f(2n) + 2 \times \left( \sum_{k=0}^{n} f(2k) \right) $$
This equation allows us to compute the number of ways to tile a $3 \times N$ rectangle using $2 \times 1$ tiles by building upon the solutions for smaller rectangles.
Deriving the closed form
Step 1: Express $g(n-1)$ Using the Second Equation
First, let's shift the index in the second equation to express $g(n-1)$ in terms of $f$ and $g$.
Replace $n$ with $(n-1)$ in the second equation: $$ g(n-1) = f(n-2) + g(n-3) $$
Step 2: Substitute $g(n-1)$ Back into the First Equation
Now, substitute this expression for $g(n-1)$ into the first equation: $$ f(n) = f(n-2) + 2 \times g(n-1) $$ $$ f(n) = f(n-2) + 2 \times (f(n-2) + g(n-3)) $$
Step 3: Simplify the Equation
Let's distribute the 2: $$ f(n) = f(n-2) + 2f(n-2) + 2g(n-3) $$ $$ f(n) = 3f(n-2) + 2g(n-3) $$
Step 4: Iteratively Substitute to Eliminate $g(n-3)$
We still have a $g$ term ($g(n-3)$) that we need to eliminate. We'll use the second equation again to express $g(n-3)$ in terms of $f$ and another $g$.
Replace $n$ with $(n-3)$ in the second equation: $$ g(n-3) = f(n-4) + g(n-5) $$
Substitute this back into our equation for $f(n)$: $$ f(n) = 3f(n-2) + 2 \times (f(n-4) + g(n-5)) $$ $$ f(n) = 3f(n-2) + 2f(n-4) + 2g(n-5) $$
Step 5: Continue the Substitution Process
We still have a $g$ term ($g(n-5)$) to eliminate. We'll repeat the substitution process.
Replace $n$ with $(n-5)$ in the second equation: $$ g(n-5) = f(n-6) + g(n-7) $$
Substitute this back into our equation for $f(n)$: $$ f(n) = 3f(n-2) + 2f(n-4) + 2 \times (f(n-6) + g(n-7)) $$ $$ f(n) = 3f(n-2) + 2f(n-4) + 2f(n-6) + 2g(n-7) $$
Step 6: Observing the Pattern
Continuing this process, we notice a pattern forming where each term involves $f$ with decreasing even indices and $g$ with increasingly negative indices. To generalize and eliminate all $g$ terms, we can iterate this substitution process until all $g$ terms are expressed in terms of $f$.
However, this can become cumbersome. Instead, we'll observe that for even values of $n$, the number of ways to tile the rectangle can be expressed in terms of previous even terms.
Step 7: Focus on Even $n$
Since $f(n) = 0$ for odd $n$, we only need to consider even values of $n$. Let’s redefine our function for even indices:
Let $n = 2m$, where $m$ is a non-negative integer. Then, we can denote $f(2m) = f_m$.
Now, our goal is to find a recurrence relation for $f_{m}$.
Step 8: Derive the Recurrence Relation
From our earlier equation: $$ f(n) = 3f(n-2) + 2f(n-4) + 2f(n-6) + \dots + 2f(0) $$
For $n = 2m$, this becomes: $$ f(2m) = 3f(2m-2) + 2f(2m-4) + 2f(2m-6) + \dots + 2f(0) $$
Similarly, for $n = 2m + 2$, we have: $$ f(2m+2) = 3f(2m) + 2f(2m-2) + 2f(2m-4) + \dots + 2f(0) $$
Now, let's write down the equations for $f(2m+2)$ and $f(2m)$:
-
Equation for $f(2m+2)$: $$ f(2m+2) = 3f(2m) + 2f(2m-2) + 2f(2m-4) + \dots + 2f(0) $$
-
Equation for $f(2m)$: $$ f(2m) = 3f(2m-2) + 2f(2m-4) + 2f(2m-6) + \dots + 2f(0) $$
Step 9: Subtract the Two Equations
Subtract the second equation from the first to eliminate the sum terms:
$$ f(2m+2) - f(2m) = 3f(2m) + 2f(2m-2) + 2f(2m-4) + \dots + 2f(0) - [3f(2m-2) + 2f(2m-4) + \dots + 2f(0)] $$
Simplifying the right side:
- The terms $2f(2m-4), 2f(2m-6), \dots, 2f(0)$ cancel out.
- We are left with: $$ f(2m+2) - f(2m) = 3f(2m) - 3f(2m-2) + 2f(2m-2) $$ $$ f(2m+2) - f(2m) = 3f(2m) - 3f(2m-2) + 2f(2m-2) $$ $$ f(2m+2) - f(2m) = 3f(2m) - f(2m-2) $$
Rearranging terms: $$ f(2m+2) = 4f(2m) - f(2m-2) $$
Step 10: Generalize the Recurrence Relation
Replacing $m$ with $n$ for simplicity, we obtain the final recurrence relation: $$ f(2n+2) = 4f(2n) - f(2n-2) $$
Dividing both sides by 2 (since we're dealing with even indices) to express it in terms of $f(n)$: $$ f(n+2) = 4f(n) - f(n-2) $$
Or, more generally: $$ f(n) = 4f(n-2) - f(n-4) $$
Final Recurrence Relation
Thus, we have successfully derived the closed recurrence relation: $$ f(n) = 4f(n-2) - f(n-4) $$
This equation allows us to compute the number of ways to tile a $3 \times N$ rectangle using $2 \times 1$ tiles by building upon the solutions for smaller rectangles.
Conclusion
We have derived the recurrence relation: $$ f(n) = 4f(n-2) - f(n-4) $$
This linear recurrence relation simplifies the computation of the number of tiling configurations without involving the auxiliary function $g(n)$.
Example Calculation
Let's compute $f(6)$ using our recurrence relation.
Given:
- $f(0) = 1$ (An empty rectangle has one way to be "tiled" — by doing nothing.)
- $f(2) = 3$
- $f(4) = 4f(2) - f(0) = 4 \times 3 - 1 = 11$
Now, applying the recurrence for $n = 6$: $$ f(6) = 4f(4) - f(2) = 4 \times 11 - 3 = 44 - 3 = 41 $$
So, there are 41 ways to tile a $3 \times 6$ rectangle with $2 \times 1$ tiles.
Share this blog
Related Posts
26-11-2024
An in-depth exploration of an efficient algorithm to compute the sum of Euler's Totient Function up ...

21-11-2024
A comprehensive guide to understanding derangements using the inclusion and exclusion principle.

18-11-2024
An in-depth exploration of perfect covers of chessboards using dominoes, including combinatorial rea...

22-07-2023
Enhance your dynamic programming skills with our comprehensive collection of Linear DP problems from...
12-07-2023
Explore efficient solutions to dynamic programming problems from the CSES problem set and other repu...
18-05-2025
Learn how to build a robust, serverless application on AWS to perform calculations like $f(x) = x^2 ...
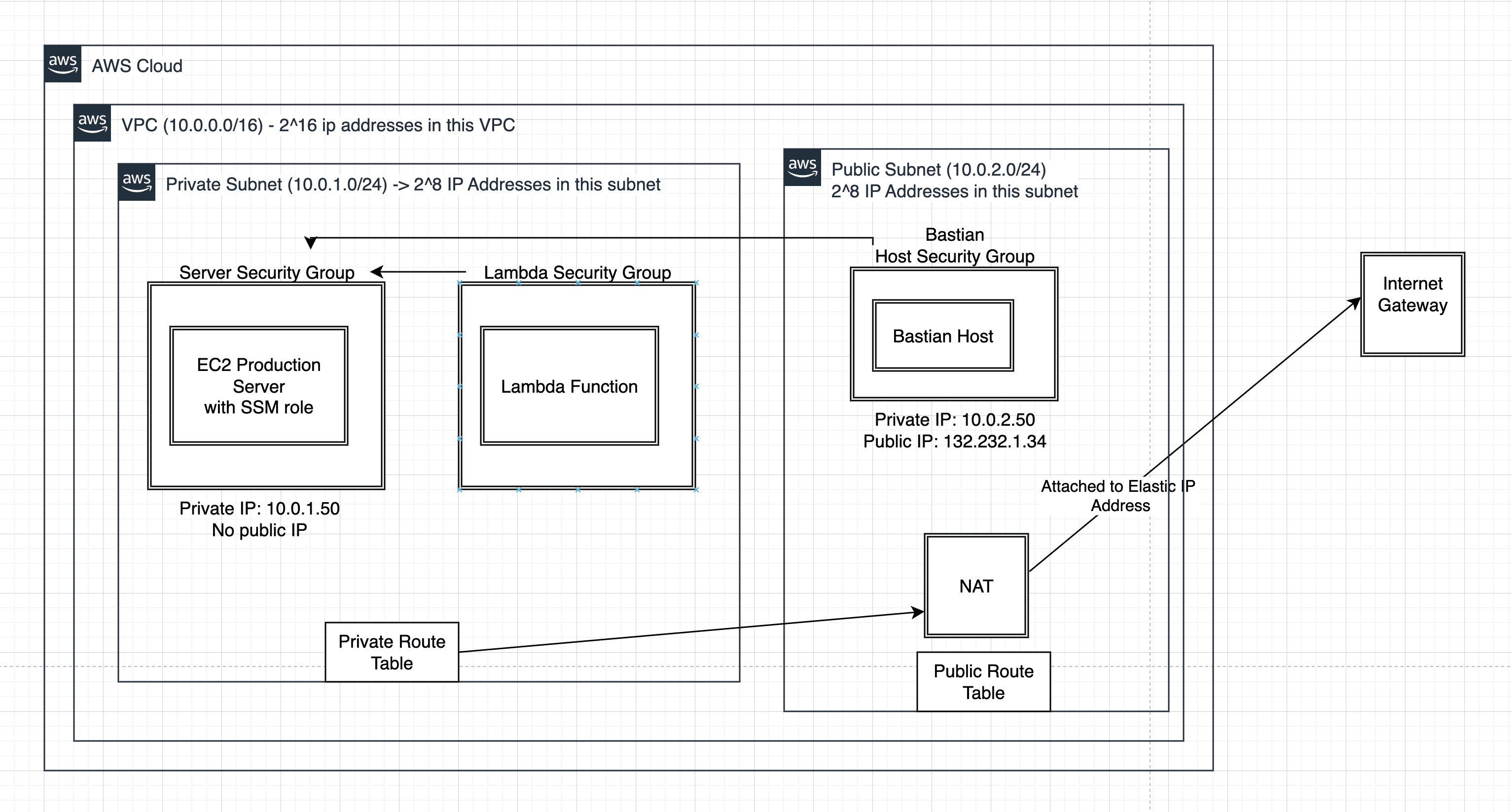
09-02-2025
In this comprehensive blog, discover how to build a production-like AWS environment with a private E...
09-12-2024
This blog is dedicated to simplifying complex mathematical and computational concepts into understan...
01-12-2024
Static Range Sum queries using various Algorithms